Разумно о фото | Архив | Школа фотографии

ШКОЛА ФОТОГРАФИИ / АРХИВ / Разумно о фото

Разумно о фото

Предисловие

В последние годы ассортимент любительских цифровых фотоаппаратов расширился в разы. Регулярно выходят новые модели, появляются и активно рекламируются новые функции. Плёночная техника тоже постоянно обновляется. В результате неподготовленному технически любителю всё труднее в этом многообразии разобраться.
  Масла в огонь подливают журналы. Одну и ту же модель могут назвать "профессиональным 5-мегапиксельным аппаратом" в одном месте и "любительской мыльницей с ограниченными возможностями" в другом. Причина очень проста: среди авторов могут быть совершенно разные люди, с разным опытом и разными критериями оценки. Встречаются и просто рефераты от "пиарщиков" и рекламистов фирмы-изготовителя, обычно очень далёкие от действительности. Продавцы в магазинах, как правило, не имеют практического опыта съёмок продаваемой техникой и ориентируются на те же журналы и рекламные проспекты. Я многократно слышал вопиюще безграмотные советы покупателям даже в центральных московских фотомагазинах. Что творится "в глубинке" мне вообще страшно представить. Смущённый покупатель заходит на форумы в Сеть, но его вопросы обычно быстро вырождаются во флейм одного из трёх-четырёх видов (примерно таких: "плёнка или цифра", "зеркалка или мыльница", "Sony или Canon"), что запутывает его ещё больше.

На самом деле причина путаницы очень проста: многогранность и многозначность всех понятий, участвующих в спорах и оценках.

1. Многогранен объект съёмки: люди (портрет), люди (репортаж), пейзаж, архитектура, животные, микрообъекты (капельки-жучки-бабочки), и т.д.
2. Различны стили фотографии, её "изюминки", грубо:
  художественные портреты и пейзажи (важно, КАК снято);
  сюжетные и репортажные снимки (важно, ЧТО и КОГДА снято, пойман уникальный момент или сюжет);
  протокольные снимки ("здесь был Вася", "я и Эйфелева башня"), причём для массового фото это - преобладающий жанр;
  макросъёмка;
  и т.д.
3. Различны требования к техническому качеству. Кому-то важнее детализация, "каждая волосинка, каждый лепесточек"; кому-то - правильные цвета, "розовая, здоровая кожа, а не землистые маски"; кого-то напрягает цветной шум, кого-то - цветные контуры, кто-то замечает геометрические искажения, кто-то - виньетирование(затемнение) по краям, кому-то важно красивое "размазывание" заднего плана в портретах. Понятно, что "хорошо быть и богатым и здоровым", но в данном случае не получается.
4. Различны требования к удобству и функциональности. В зависимости от личных привычек, характера и стиля фотографии на первый план могут выходить отдельные факторы из длинного списка:
  возможность быстрого контроля результата;
возможность кадрировки в широких пределах, не сходя с места (широкоугольность и кратность зума);
  скорость автофокуса, промежуток от нажатия на кнопку до кадра;
  точность экспоавтоматики;
  возможность оперативно корректировать ББ, контраст и шарп или даже вообще о них забыть (съёмка в RAW);
  возможность ручной установки диафрагмы или выдержки, ручного фокуса;
  "скорострельность";
удобство кадрировки;
  удобство ношения (компактность и вес);
  расширяемость;
  автономность;
  прочность и непромокаемость;
  и т.д., и т.п.
5. Немаловажен и вопрос цены. Причём не только аппарата, но и всего дальнейшего процесса и расходных материалов. При разной "фотоактивности" сравнение только цен камер не совсем корректно.
Интересный момент: если некоторые параметры однозначно ложатся на шкалу "лучше-хуже" (например, цена или точность цветопередачи), то оценка некоторых зависит исключительно от жанра фотографа. Например, большая глубина резкости у аппаратов с маленькими матрицами - хорошо или плохо? Очень хорошо - если речь о макросъёмке. Очень плохо - если о художественном портрете.
Главный вывод из вышеизложенного: невозможно корректно ответить не только на самые "общие" вопросы типа "что лучше - плёнка или цифра", но даже на менее общие типа "что лучше - фотоаппарат А или фотоаппарат Б?". Для каждого фотографа, в зависимости от его вкуса, стиля и потребностей ответ будет свой. НЕТ ЛУЧШИХ, ЕСТЬ ОПТИМАЛЬНЫЕ конкретно для Вас, под конкретные задачи и в конкретных условиях.

В данной статье я попытаюсь описать в общих чертах основные параметры фотоаппаратов и их влияние на конечный результат. Я надеюсь, это поможет сделать оптимальный ДЛЯ ВАС выбор.

Объектив. Диафрагма. Светосила, ГРИП и аберрации.

          Объективы простые и сложные. Диафрагма и аберрации.

Изображение на плёнке (в "традиционном" фотоаппарате) или на матрице (в цифровом) рождается объективом. От его свойств во многом зависит результат. С объективов и начнём...

Простейший объектив (монокль) состоит из одной линзы. Известная из школы формула геометрической оптики связывает расстояния от линзы до объекта с расстоянием от линзы до его изображения так: 1/L+1/d=1/F, где F называется (по определению) фокусным расстоянием. В частности, бесконечно далёкие объекты будут "фокусироваться" именно на этом расстоянии (d=F). В теории всё выглядит замечательно - любая точка переходит в точку, плоскость - в плоскость. На практике всё гораздо сложнее, и по краям изображения в любой лупе мы видим цветное размазанное месиво вместо чёткой картинки. Это связано с тем, что известная формула выведена (и справедлива) лишь для тонких приосевых пучков монохроматического света. Подобно тому, как сложную кривую вблизи каждой точки можно "приблизить" касательной (математики это называют рядом Тейлора), сложную формулу реальной линзы "приближают" простой формулой геометрической оптики тем точнее,
1. чем меньше диаметр "работающей" части линзы,
2. монохроматичнее освещение (преломление стекла зависит от цвета луча, а вместе с ним и фокусное расстояние, поэтому лучи разных цветов от одного и того же объекта сфокусируются, вообще говоря, в разных местах)
3. ближе объект к оптической оси. Назовём это условиями применимости упомянутой формулы. Отклонения от "идеальной" формулы принято называть аберрациями. Их несколько видов, но подробно рассматривать мы их не будем. Разделим только на "хроматические" и "геометрические". Если вспомнить аналогию с рядом Тейлора, то геометрические аберрации (очень грубо) вызваны "нелинейными" членами более высоких порядков. При этом "малыми" переменными являются толщина пучка (условие применимости 1) и угол объекта от оси (условие применимости 3), а от геометрии линзы зависят коэффициенты при этих переменных. Если закрыть края линзы непрозрачной пластинкой с отверстием по центру, толщина пучка уменьшится, условие применимости 1 начнёт лучше выполняться и при любой геометрии линзы, т.е. при любых коэффициентах, часть искажений уменьшится. Упомянутая пластика с отверстием называется диафрагмой. Уменьшение отверстия называют "закрытием", а увеличение - "открытием" диафрагмы. Измеряют степень диафрагмирования безразмерным числом диафрагмы, равным отношению фокусного расстояния к диаметру отверстия. Типичные значения - от 2 до 16 (стандартные значения следуют с шагом в корень из двух: 2, 2.8, 4, 5.6, 8, 11,16), хотя бывает и 1,4 и 32. Запомним пока важный вывод: с закрытием диафрагмы аберрации любого объектива уменьшаются.

Но закрытие диафрагмы не всегда допустимо, т.к. влияет на экспозицию и глубину резкости (далее - ГРИП, или Глубина РезкоИзображаемого Пространства), мы об этом влиянии поговорим немного позже. Да и угол зрения не всегда малый (например, в "широкоугольниках"). Т.е. наши "малые" переменные не всегда безболезненно можно уменьшить. Остаётся работать с коэффициентами при них. Оказывается, что для разных форм линз и разных сортов стёкол коэффициенты имеют не только разные значения, но и разные знаки, поэтому если сделать объектив из нескольких линз, коэффициенты некоторым образом суммируются и можно подобрать конфигурацию так, что суммарные аберрации системы линз на порядок меньше чем каждой в отдельности. Примерно таким же образом можно бороться и с хроматическими аберрациями - применением линз с разным знаком т.н. "дисперсии"(различного отклонения лучей разного цвета). Именно поэтому реальные объективы обычно состоят из трёх и более элементов. Теоретически, увеличивая количество элементов, можно последовательно уменьшать все аберрации. Однако в игру вступают другие факторы: рассеяние в стекле, переотражение от поверхностей и накопление ошибок в изготовлении/сборке. Чем больше элементов, тем лучше должно быть качество стекла, качество просветления (напылённый слой для уменьшения переотражений), качество и точность сборки, что заметно увеличивает массу объектива и ещё более заметно - его стоимость. Обычно сложные объективы имеют не более 10-15 элементов. Если же нужно рассчитать объектив с переменным фокусным расстоянием (в просторечии - "зум"), задача сильно усложняется. Если раньше нужно было "подбирать" коэффициенты под несколько расстояний от объекта, под несколько углов (или расстояний до оси) и при нескольких (обычно - трёх) длинах волн, то теперь всё то же самое, но ещё и при разных фокусных расстояниях! Как правило, невозможно "равномерно" устранить каждый вид аберрации при всех положениях зума - какая-то больше на "широкоугольном" конце, какая-то - на "длинном". И чем больше отличаются фокусные расстояния (т.е. чем больше "кратность зума") - тем менее выполнима задача.

Вспомним про диафрагму. Поскольку коэффициенты нижних порядков в большой степени скомпенсированы, рост искажений с открытием диафрагмы может быть гораздо круче линейного. Иными словами, если объектив удовлетворительно скомпенсирован при диафрагме 5,6, при отверстии 4 искажения могут стать заметны, а при 2,8 - невыносимы. Отсюда следует два вывода:
один из наиболее часто применяемых способов удешевления объективов при сохранении удовлетворительных искажений - ограничение диафрагмы средним (около 5,6) или даже высоким(8-11) значением.
как правило, любительские объективы проектируются так, чтобы при максимально открытой диафрагме (она ещё называется светосилой) аберрации были равны предельно допустимым по стандарту,( т.е. вполне заметны, хотя не вопиющи). Больше - честь фирмы не позволяет, а меньше - очень дорого. Но стоит "отступить" пару делений - и искажениями вполне можно пренебречь. Так что если нужно получить чётко проработанные кадры, как правило, лучше прикрыть диафрагму на пару делений от полностью открытой. Разумеется, если нет других противопоказаний (если мало света, или нужно размыть фон, или нужна короткая выдержка - диафрагму, конечно, открывают полностью).
Нетрудно из последнего вывода сделать и ещё один: если оставаться внутри одного "класса" оптики (например, "любительского"), то из двух объективов с одинаковыми фокусными расстояниями(или одинаковым диапазоном фокусных расстояний) на одной и той же диафрагме качественнее будет более светосильный.

Подведём итоги. Проектирование объективов - сложный поиск компромисса между ценой, весом, искажениями, светосилой и кратностью зума. Параметры могут варьироваться в широких пределах и улучшение каждого из них немедленно ухудшает остальные.
Например:
   При одинаковой цене и светосиле чем больше кратность зума, тем ниже качество. Максимальное качество - у "фиксов"(объективов с постоянным фокусным расстоянием)
   При одинаковом качестве чем больше кратность зума, тем меньше светосила
   При одинаковом зуме (или фокусном расстоянии) чем больше светосила, тем выше цена. Каждое деление диафрагмы может удвоить-утроить цену!
И так далее. Не может быть объектива с высокой кратностью зума, светосильного, качественного, лёгкого и дешёвого ОДНОВРЕМЕННО!

                  Виды и маркировка объективов.

В зависимости от угла зрения, объективы традиционно делят на широкоугольные, нормальные и длиннофокусные. Из элементарной геометрии следует, что угол зрения зависит от отношения фокусного расстояния (далее - ФР) к диагонали матрицы (или плёнки), но в связи с широкой распространённостью плёночного формата "35мм" принято характеризовать объектив не углом, а так называемым "эквивалентным фокусным расстоянием" (далее - ЭФР). Для плёнки ЭФР просто равно истинному, т.е. ФР. "Нормальные" объективы имеют ФР около 50мм, широкоугольные 28-35мм, более короткофокусные обычно называют сверхширокоугольными. Длиннофокусные объективы обычно имеют 100-300мм. Длиннее в любительской практике не встречается. Отдельно стоит отметить ФР 80-100мм - их часто называют "портретниками". Именно с этими объективами лицо человека крупным планом имеет наиболее естественную перспективу. У цифровых матриц с диагональю меньшей, чем у плёнки, для обеспечения того же угла зрения (и соответственно того же кадра с того же места) истинное фокусное расстояние объективов делают пропорционально меньше. Так, для матриц с диагональю 9мм (т.н. 1/1,8" матрицы), нормальным будет объектив 10мм, портретником будет 16-20мм, а 35мм - уже полноценным "телевиком". Таким образом, в характеристиках аппарата мы можем увидеть два разных ФР - истинное и эквивалентное. К примеру, довольно распространён зум с ФР=7-21мм и ЭФР=35-105мм.

На оправе обычно пишут через дробь ФР и светосилу, например 50/1,4 или 7-21/2,0-2,8. В последнем случае надпись означает, что светосила при 7мм равна 2,0, а при 21мм - 2,8. Очень часто диафрагму пишут не как число (например, 8), а как дробь с буквой F (например, F/8). Так же в технических данных обычно кроме светосилы пишут диапазон диафрагмирования, например для цифровых мыльниц типично F/2-F/8. В результате часто в обзорах, особенно сравнительных, диапазон значения диафрагмы путают либо с диапазоном светосилы, либо вообще с фокусным расстоянием (из-за буквы F). Я уже неоднократно встречал "светосилу" 2-8 (вместо 2-2,8) в сводных таблицах, причём только у некоторых аппаратов в таблице, у других значения были правильными. Такие "опечатки" могут сильно повредить при сравнительном выборе камер. Так же я неоднократно (хотя и реже) встречал "фокусное расстояние" 2-8мм (вместо тех же 7-21например).

Повторю на всякий случай, что светосила - это значение максимально открытой диафрагмы. Таким образом, если написано что у объектива 7-21мм/2,0-2,8 диафрагмы 2,0-8,0 , это означает что при 7мм диапазон диафрагм 2-8 (и светосила = 2,0), а при 21мм диапазон 2,8-8 (и светосила = 2,8).

Вернёмся к углам зрения. Для большинства любительских съёмок достаточно "нормального" объектива (ЭФР=50мм), т.к. его охват пространства близок к естественному восприятию глаза. Разумеется, иногда хочется вместить в кадр побольше (пейзаж, тесное помещение), а иногда, наоборот "наехать поближе"(крупный портрет или деталь при невозможности подойти). Поэтому обычно в качестве основного (а у большинства аппаратов - и единственного) объектива применяется зум с диапазоном "вокруг" нормального, например с ЭФР 35-90 или 35-105. Отношение "длинного" ЭФР к "короткому" называется кратностью зума, меряется в буквах "х" и часто гордо указывается на корпусе, особенно для плёночных мыльниц с длинными "хоботами". Многие считают, что чем больше "х", тем лучше. Почему это не так, мы обсудим в следующей главе. Если же вы собираетесь снимать нечто специальное (особо широкие пейзажи или наоборот - фотоохота), стоит подумать о сменных широкоугольнике/телевике. Суперкратные зумы конечно частично спасают положение, но обычно ценой либо качества, либо светосилы (об этом уже говорилось выше). То же относится и к "насадкам" на штатный объектив. Любой специализированный "ширик"/"телевик"/"макрик" снимает заметно лучше, чем универсальный зум с насадками.

                        Диафрагма и экспозиция.

Как химические (в плёнке), так и электрические(в матрице) процессы фиксации изображения требуют определённого количества света для своей работы. Чем меньше это количество - тем выше т.н. чувствительность плёнки/матрицы. Измеряется она в так называемых "единицах ISO". Типичные значения - 100, 200, 400, но бывают и меньше/больше. Для получения одинаково "серого" цвета на плёнку(матрицу) чувствительностью ISO400 нужно подать вчетверо меньше энергии света по сравнению с ISO100. Обсуждение самих чувствительностей (и их оборотной стороны - шумов) мы отложим до главы о размере матриц, а пока вернёмся к диафрагме. Итак, при заданной чувствительности нам нужно подать на матрицу заданную энергию, которая, как известно равна произведению яркости на время действия (т.н. выдержка). Таким образом, меняя выдержку, мы не только "замораживаем" движение, но и "дозируем" свет. А вот яркостью как раз управляет диафрагма - яркость обратно пропорциональна квадрату диафрагменного числа. Т.е. диафрагма 2 пропускает вчетверо больше света, чем диафрагма 4. Именно поэтому диафрагму маркируют по степеням корня из двойки (т.н. "деления" или "стопы") - каждый стоп изменяет яркость вдвое. Сочетание выдержки и диафрагмы (с точки зрения энергии пропущенного света) называют экспозицией. Совершенно очевидно, что для одной и той же внешней освещённости существует не одна "верная" экспозиция. Например, 2,0*1/2000c=2,8*1/1000c=4,0*1/500c=5,6*1/250c=8*1/125c=11*1/60c=16*1/30c (знак умножения здесь условен, обозначает лишь сочетание). Все эти экспозиции ОДИНАКОВЫ, т.е. дадут одинаковый по яркости результат. При бОльшей освещённости нужно ещё укоротить выдержку или прикрыть диафрагму и наоборот - при меньшей - удлинить выдержку или приоткрыть диафрагму. Таким образом, диафрагма при одних и тех же внешних условиях влияет на выдержку, т.к. они жёстко связаны между собой "верной" экспозицией. Иногда это полезно - например, при съёмке быстрых движений и спорта мы можем полностью открыть диафрагму - тогда выдержки станут максимально короткими и не будет "смаза" от движения объектов. И наоборот...

Кроме смаза от движения объекта, существует ещё т.н. "шевелёнка" - дрожание рук фотографа. Она коварна тем, что не поддаётся строгому измерению, т.к. является случайным процессом. Но "народный опыт" вывел очень усреднённое правило - шевелёнки следует бояться при выдержке (в сек) длиннее, чем 1/ЭФР(в мм). Т.е. при ЭФР=105мм лучше длиннее, чем на 1/100 без штатива не снимать. Таким образом, чем более длиннофокусен объектив, тем важнее ему иметь достаточную светосилу, т.к. длинные выдержки ему недоступны из-за шевелёнки (штатив пока не рассматриваем). И вот тут-то самое время вспомнить про "хоботы" "особопродвинутых" плёночных мыльниц. 35-140, 35-160, 35-200мм! "Круто"?! Пустые цифры и выброшенные деньги. Для сохранения компактности диаметр этих хоботков остался прежним, следовательно, светосила на "длинном" конце доходит до 12-16. Поскольку снимать можно только короче чем 1/200 - это только очень яркие объекты на ярком солнце. Как только оно зайдёт за тучку или объект уйдёт в тень - начнётся шевелёнка. Не говоря о вечере. Таскать же штатив вместе с компактной камерой слегка странно - проще иметь недорогую зеркалку, разница в размерах и весе гораздо меньше чем нормальный штатив. А про оптическое качество с повышением кратности зума уже было сказано выше.

Подведём краткий итог: диафрагма позволяет управлять экспозицией, и при фиксированном освещении жёстко связана с выдержкой - чем "открытее" диафрагма, тем короче выдержка. Чем выше светосила, тем в более тёмных условиях можно снимать (при фиксированной выдержке) либо тем с более короткой выдержкой можно снимать (при фиксированной освещённости). Далее значение диафрагмы, влияющее на экспозицию, мы ещё будем называть яркостной диафрагмой (ниже будет понятно почему).
Кстати, возвращаясь к определению диафрагмы, можно, наконец, дать его более строго. Мы ведь рассматривали одну линзу с одной "дыркой", и самый тонкий диаметр пучка совпадал с физическим диаметром отверстия. Реальные объективы имеют много линз с разными диаметрами, и не всегда отверстие диафрагмы находится физически в самом тонком месте на самой маленькой линзе. Как же тогда определяют и градуируют диафрагменные числа? А очень просто - через яркость. Т.е. некоторое положение реальных лепестков диафрагмы соответствует такому числу, какое бы дала одна тонкая линза с той же яркостной диафрагмой (т.е. пропускающая столько же света).
Диафрагма и ГРИП.По законам оптики расстояния от объектива до плёнки и до объекта съёмки жёстко связаны. Если мы хотим "навести" объектив скажем на объект в 3м от аппарата, мы (вручную или средствами автоматики) передвигаем его относительно плёнки(матрицы) на нужное расстояние - это и называется фокусировка (в автоматическом случае - "автофокус"). А что же происходит с объектами "не в фокусе", например на расстоянии 3,5 метра? Из элементарной геометрии следует, что каждая точка вместо точки сфокусируется в пятнышко, тем большего диаметра, чем более открыта диафрагма и чем сильнее удалён объект от "правильного" расстояния(на которое сфокусирован объектив). Практика показывает, что средний человеческий глаз при рассматривании фотографий 13*18см практически не различает разницы для диаметра пятнышка около 1/1500 диагонали кадра. Применяя элементарную геометрию и формулы линзы, несложно вывести формулы для тех расстояний, для которых пятно нерезкости будет в точности равно 1/1500 диагонали. Всё что между ними будет изображаться "практически резко". Если "дальнее" из двух расстояний конечно, то разницу между ним и "ближним" принято называть ГРИП (Глубина Резко Изображаемого Пространства). Формула для неё довольно громоздка, но, к счастью, в некоторых типичных случаях легко упрощается. Рассмотрим три основных случая - "пейзажный", "портретный" и "макро". Но предварительно введём два более удобных во многих случаях параметра:
Kf - отношение диагонали 35мм кадра к диагонали матрицы ("обобщённый кропфактор"). Для плёночных фотоаппаратов равен 1. Для Canon 10D/300D равен 1.6. Для матриц 2/3"(SONY717, SONY828) равен примерно 4, для матриц 1/1.8" - пяти. Ну и так далее...

ВНИМАНИЕ! Не пытайтесь вычислять диагонали матриц из их "дюймовых" обозначений! Исторически сложилось так, что там несколько другие, "видиконовые", дюймы. Впрочем, они меньше стандартных примерно в 1,7 раза и если поделить результат на 1,7, получится близкая к истине диагональ... Поэтому, хоть по своей сути Kf - характеристика размера матрицы, гораздо проще и точнее рассчитывать её по приводимым в документации или рекламе характеристикам объектива - из элементарной геометрии следует, что Kf=ЭФР/ФР! ЭФР обычно указывают в рекламе (ну, к примеру, 35-105мм), ФР у уважающей себя фирмы нарисовано на объективе (скажем, 7-21мм). Для приведённого примера, очевидно, Kf=105/21=35/7=5.

P - размер(диагональ) ОБЪЕКТА (в простейшем случае когда мы снимаем картинку на стене - диагональ того прямоугольника, который влез в кадр). Измеряем в метрах. Типичные значения скажем для портрета - 1метр, для лица самым крупным планом - 0,5м, для макро - сантиметры, для портрета "в рост" - 2,5-3м и так далее.

ВНИМАНИЕ! Очень часто этот параметр (P) гораздо важнее чем "дистанция фокусировки L", которая упорно входит во все учебники, т.к. именно P отражает КОМПОЗИЦИЮ (компоновку) кадра, т.е. ЦЕЛЬ снимающего. Часто нам совершенно неважно с какого расстояния снимать, важно ЧТО снимать. А вот при одном и том же P дистанция сильно зависит от ЭФР объектива, т.е. не является константой при сравнении разных объективов. Упорное непонимание этого факта рождает стойкие мифы, к которым мы ещё вернёмся при рассмотрении "портретной" зоны.

Пейзажная зона.

Пусть L - дистанция фокусировки (расстояние до объекта). При L=бесконечность резкими будут не только объекты на бесконечности, но и на всех расстояниях больших некоторого расстояния H, получившего название "гиперфокальное" расстояние. Из упоминавшихся "сложных" формул оно легко выводится, получается хрестоматийное выражение
H = Fист2/(A∙c), где
Fист-истинное (не эквивалентное!) фокусное расстояние, метры (оно же - ФР).
A - диафрагменное число
c - допустимый кружок нерезкости, 1/1500 диагонали матрицы (метры).
Но нетрудно вывести и более удобную и универсальную формулу, учитывая, что Fист=ЭФР/Kf, а с=0.042/1500/Kf (0.042метра-диагональ плёночного кадра).
Подставив и округлив, получим
H = (0.19∙ЭФРмм)2/(Kf∙A), где, ЭФРмм-это значение ЭФР в миллиметрах, а H получается в метрах.
При уменьшении L от бесконечности до H "дальняя" граница резкости остаётся бесконечной, а ближняя уменьшается до H/2.
При L=H ГРИП "максимальна" - от Н/2 до бесконечности. Таким образом, выставив объектив на гиперфокальное расстояние, мы получаем максимально возможный для этого значения диафрагмы охват - от половины гиперфокального расстояния до бесконечности. Этим часто пользуются изготовители самых дешёвых мыльниц (а также веб-камер и камер наблюдения) для экономии на системе фокусировки. Широкоугольный объектив жёстко крепится сфокусированным на гиперфокал.

Очевидно, что если пейзаж имеет не только "дальние" объекты, но и средний и, тем более, ближний план, диафрагму лучше прикрыть. Видно, однако, что если у плёночных аппаратов для хорошей проработки многоплановых (с объектами на переднем плане) пейзажей нужно закрывать диафрагму до 8-11 (а на длинных фокусах и более), то у цифрокомпактов пейзаж "начинается от порога" - на "коротком"(ЭФР=35мм) конце зума даже на диафрагме 4 всё резко от метра до бесконечности. Этим иногда можно пользоваться в репортажных целях - отключив автофокус (если это позволяет камера!) и наводясь на гиперфокальное расстояние. Экономит ценные доли секунд!

Портретная зона. Fист«L«H

Общая формула сильно упрощается, вот так:
ГРИП=2*A*c/M2 Здесь М - масштаб, отношение размера изображения к размеру реального объекта. Поскольку как c, так и М зависят от размера матрицы, вновь перейдём к моим "фирменным" переменным Kf и P. После несложных подстановок, получаем
ГРИП=(Kf*A)*P2/32
32 в знаменателе - размерная величина (метры, получена из диагонали плёночного кадра), так что с размерностью всё в порядке. Оставив обсуждение значения Kf до следующего раздела, отметим другую важную деталь - если мы хотим снять некий объект, занимающий фиксированную часть кадра (ну скажем портрет, P=1метр), т.е. размер P фиксирован (а для портретной съёмки это - типичная ситуация), то ГРИП не зависит ни от фокусного расстояния объектива, ни от расстояния до объекта, только от диафрагмы. Это воспринимается в штыки большинством фотографов, приученных к расхожей (неверной!) поговорке что "у телевиков ГРИП меньше чем у широкоугольников". Эта поверхностная поговорка справедлива для фиксированного расстояния до объекта. Но при изменении фокусного расстояния и прежнем расстоянии до объекта мы сравниваем фактически разные кадры - например, портрет в полный рост и глаза крупно. Это совершенно разные стили и сравнение теряет всякий смысл. Единственное что имеет смысл - это сравнение одинаковых по построению кадров (например, "лицо и плечи", грудной портрет, P=1метр). Мы можем снимать его близко, нормальным объективом, можем отойти подальше и снимать телевиком, но ГРИП от этого не изменится (при одинаковой диафрагме). С этим не все сразу соглашаются, но это так. И не только из сухих формул - это легко подтверждается практикой.
Другой важный вывод - ГРИП прямо пропорциональна диафрагме. Т.е. если мы хотим "размыть" фон и придать портрету объём, мы диафрагму должны максимально открыть. Если же резкий фон почему-либо важен - наоборот, прикрыть.
Легко посчитать, что для типичного портрета (P=1м) и диафрагмы 2,8 мы имеем ГРИП около 9см на плёнке и целых 45см на цифрокомпактах с матрицей 1/1.8".
Макрозона. Fист~L.
Для "неглубокого" макро (P более 4см для плёнки и более 1см для цифрокомпактов) вполне удовлетворительное приближение даёт формула из "портретной" зоны. Приводить же точную формулу для "глубокого" макро я не вижу смысла, т.к. там всё равно требуются поправки на непостоянство светосилы от масштаба и толщину объектива, да и редко встречается такое макро у любителей. Итак,
ГРИП~(Kf*A)*P2/32
Если мы снимаем скажем пятисантиметровый объект, P=0.05 то на плёнке ГРИП будет от 0,2мм (A=2) до 2мм (A=22). На цифрокомпакте типа G5 ситуация получше - от 1мм (А=2) до 4мм(А=8). Но общая тенденция одна - ГРИП слишком мала и приходится максимально возможно закрывать диафрагму. ГРИП по-прежнему прямо пропорциональна диафрагме.
Раз уж мы заговорили о "макро", отмечу очень важный факт: во всех без исключения рекламных и технических параметрах указывается вопиюще неграмотный параметр - минимальное расстояние до объекта. При условии разных фокусных расстояний и конструкций объективов этот параметр не значит ровно ничего. Аппарат А с расстояния 1см может снимать мельче(т.е. с меньшим увеличением) чем аппарат Б с 10см. Иногда (особенно в плёночной фотографии) вместо расстояния в качестве характеристики макрообъектива указывают масштаб съёмки. Но в связи с разными размерами матриц этот параметр также не годится. Единственно верным и корректным параметром, характеризующим макровозможности камеры следует считать Pmin - минимальную величину объекта, показанного во весь кадр. Для этого просто достаточно взять в магазин линейку и снять её во весь кадр. Например, вот так:

Для данного снимка Pmin~5мм.
Не расстраивайтесь, если у Вас получится сильно больше - этот снимок сделан отнюдь не штатным объективом, применялись кольца, насадочные линзы и т.п.

Размер матрицы. Шумы и цветопередача. Влияние на ГРИП.

Шум

К сожалению, маркетинговый приём "народ покупает мегапикселы" действует вовсю. 90% людей на вопрос "каков размер матрицы у аппарата Х?" ответят - "Y Мегапиксел!". А между тем гораздо важнее не мегапикселы, а миллиметры. Именно они определяют площадь поглощения света и многие другие, связанные с этим, характеристики матрицы. И, прежде всего, - её шумы. Дело в том, что у матрицы (в отличие от плёнки) чувствительность можно выставлять в меню. Но наличие в меню строчки "400"(или даже "800") на самом деле ничего не говорит о сравнительной чувствительности матрицы. С ростом выставляемой чувствительности растут и шумы, и только от совести производителя зависит при каком уровне шума он решит остановиться. Т.е. корректнее сравнивать чувствительность на одинаковом уровне шумов. И тут может оказаться, что камера А на своих ISO800 шумит так же, как камера Б на ISO100. При этом, разумеется, без слёз глядеть на результаты камеры Б при ISO800 уже невозможно. Отсюда следует простой вывод - не стоит обращать внимание на декларированный набор чувствительностей. Просто надо забыть про него. Лучше смотреть уровень шумов в независимых обзорах. При прочих равных, разумеется, меньше шумят большие по размерам(в миллиметрах, а не в пикселях!) матрицы. Итак, чем меньше геометрически матрица, тем выше её шумы и (следовательно) ниже реальная чувствительность. В качестве иллюстрации приведу старый сравнительный тест G2(Кf=5) против D60(Kf=1.6), хорошо видна разница в цветах и шумах при одной и той же чувствительности и экспозиции:

Не стоит очень пугаться серых цветов у G2 - объект находился в глубокой тени (снят против света), у хорошо освещённых объектов всё будет не так мерзко.

Часто можно встретить мнение, что при одном и том же геометрическом размере матрицы многомегапиксельные шумят больше (т.к. меньше размер каждого пиксела). Это совершенно справедливо если сравнивать кропы попиксельно (скажем фрагмент 100*100 пикселей от каждой камеры). Но это не совсем корректно, т.к. сравнивать надо конечные ОТПЕЧАТКИ одного размера, т.е. одинаковые ДОЛИ кадров (например, сделав ресайз одинаковых долей кадров до одинаковых размеров). При таком подходе различие уже не столь заметно и гораздо меньше колебаний, связанных с разными настройками встроенного шарпенинга (о шарпенинге подробнее чуть позже, в разделе про разрешение).

Цветопередача

Тут сложнее объяснить на пальцах, но цвета с бОльших матриц явно чище, переходы между ними более "натуральные". Речь не об ошибках баланса белого, который легко компенсируется. Речь о микроуровне, который, однако легко начинает бросаться в глаза при съёмках человеческой кожи, особенно - детской. И особенно - при печати на фотобумагу.
Ну и про пропадание цветов в тенях Вы уже видели на примере чая Липтон...
Тем не менее, типичные любительские "фотки"(пейзажи, архитектура, репортаж) снятые ясным днём вполне качественно печатаются 10*15 даже с самых бюджетных цифромыльниц. Т.е. проблема цветопередачи явно есть, но она не встречается на каждом шагу и не стоит её драматизировать. Просто полезно знать о её существовании и представлять возможности разных камер.

ГРИП и матрица

Если Вы внимательно посмотрите на формулы из раздела про ГРИП и диафрагму, то окажется, что везде диафрагма входит исключительно в паре с обобщённым кропфактором Kf, вот так: "(Kf*A)". Введём новое обозначение:
Aрезк=Kf*A - "резкостная диафрагма".
Таким образом, она равна "яркостной" диафрагме для 35мм-плёнки, и больше неё в Kf раз для матриц. Нетрудно показать, что во все формулы для ГРИП входит именно "резкостная" диафрагма. Таким образом, можно говорить не только об "эффективном фокусном расстоянии" но и об "эффективной с точки зрения резкости" диафрагме. С точки зрения ГРИП любой цифровой фотоаппарат снимает так же, как плёночный с диафрагменным числом в Kf раз большим
Получается например что замечательный на первый взгляд объектив 7-28/2-2,8 из-за матрицы в 1/1,8" "превращается" с точки зрения ГРИП в объектив, эквивалентный 35-140/10-14, т.е. хуже многих "хоботков"! (по яркости и экспозиции всё остаётся как было) И это превращение связано исключительно с геометрическим размером матрицы - оно не зависит ни от фирмы-изготовителя, ни от качества, ни от цены. Это - неумолимые законы физики. Это не всегда хорошо и не всегда - плохо. Нужно просто понимать чего Вы лишаетесь и что приобретаете. Чем мельче матрица, тем больше ГРИП - это очень хорошо для макро и пейзажей. Особенно - для макро. Несчастные "плёночники" вынуждены ставить дырки 22 и даже 32, что приводит к длинным выдержкам, громоздким штативам или дорогущим кольцевым вспышкам. Владелец же цифрокомпакта может ставить диафрагму впятеро меньше (т.е. выдержку в ДВАДЦАТЬ ПЯТЬ раз короче!!!). Т.е. практически снимать с рук без штатива и вспышек. Но с портретами ситуация обратная. У "мелких" матриц ГРИП не получается сделать маленькой, в результате на портретах гораздо чётче проработан фон (это отвлекает), а само лицо вообще не имеет градаций резкости, что делает картинку более "плоской". Бытует мнение, что "размытие фона", "боке" и т.п. при съёмке - удел профессионалов, а любителю типа и в фотошопе можно фон размыть. Это в корне неверно. Всё в точности наоборот. Как раз профессионал сможет "сгладить" дефекты чрезмерной ГРИП с помощью подбора соответствующего студийного фона и освещения. У любителя же нет такой возможности - наиболее ценны для него не "студийно-заказные", а "живые" кадры, из реальной жизни, где нет возможности управлять ни фоном, ни освещением. И именно в таких ситуациях маленькая ГРИП сильно выручает. А "фокусы" Фотошопа сделанные неумелыми "любительскими" руками смотрятся обычно очень неестественно. Да и времени отнимают много, а его обычно не хватает...

В качестве иллюстрации применения малой ГРИП я наугад выбрал из своего архива несколько портретов. Ни один из них не был постановочным, все "репортажные". Никакой обработки в фотошопе (кроме самой общей - уровни, ресайз и т.п.) не проводилось. Особенно подчеркиваю это для последнего снимка - размытая окантовка получилась при съёмке сама, это - сетка и борта манежа. Крайне рекомендуется смотреть "большие"(600*900, около 60К) варианты, т.к. маленькие превьюшки дают очень приблизительное представление и сильно пожаты

Все снимки сняты D60 (Kf=1.6) на диафрагме 1.8 (объектив 50/1.8). Они не претендуют на высокое звание "художественных", это - обычный семейный альбом. Однако за счёт малой ГРИП объём передаётся весьма неплохо... По крайней мере для любительского фото.

Обратите внимание, что я почти нигде не упомянул мегапиксели. Это - не случайно. Болезненное пристрастие к подсчёту мегапикселей сохранилось по инерции с тех дремучих (хоть и хронологически совсем недавних) пор, когда двухмегапиксельная камера была предметом мечтаний, а крепкий "середнячок" гордо красовался надписью 1,3Мп на корпусе. В нынешних условиях, когда практически даже самая бюджетная камера имеет 3 Мпиксела, а значения 4 и 5 довольно типичны, для большинства любительских нужд на первый план выходит не разрешение матрицы, а другие параметры - шумы, цвета, чувствительность, ГРИП и т.п. Это связано с тем, что влияние этих параметров хорошо видно на отпечатках ЛЮБОГО размера, даже 10*15. Даже на приведённых выше портретах размером всего лишь полмегапиксела хорошо виден характер нерезкости, объём и передача цветов. Для выявления разницы между 4- и 5- мегапиксельными матрицами одинакового (геометрического) размера пришлось бы печатать тесты как минимум 20*30, что не часто случается в обычной любительской практике.

Размер матрицы и дифракция.

Аппараты с маленькой матрицей и большими мегапикселами подстерегает ещё одна напасть - дифракция. Из-за волновой природы света строгие "точки" геометрической оптики размываются в дифракционные пятнышки. Характерный размер этих пятнышек в микронах - A/2 (более строго - длина волны*A*коэффициент порядка единицы, зависящий от критерия разрешимости, можете поискать в Сети по фразе "пятно Эйри"). Напомню, что А - значение диафрагмы. Т.е. для типичных значений 2-8 размеры соответствующих пятен - 1-4микрона. Много это или мало? Посчитаем. Возьмём "типичный" размер картинки в 5Мпиксел, т.е. грубо 2000точек по высоте. Для плёнки (Kf=1) с её высотой 24мм(24000микрон) получается шаг точки = 24000/2000=12микрон. Для Kf=4 - 3микрона, для Kf=5 - 2.4микрона. Таким образом "замыливание" картинки дифракцией на матрицах 1/1.8" и 2/3" начинается уже с диафрагмы 8, в то время как у 300D(Kf=1.6) - только с 22. Если вспомнить, что аберрации "устаканиваются" лишь в двух стопах от светосилы, которая у цифрокомпактов равна обычно 2-2,8 , то получается, что дальнейшее (более 5Мп) наращивание мегапикселей на матрицах 1/1,8" и 2/3" не имеет практического смысла, только маркетинговый. При бОльшем количестве мегапикселей дифракция начнёт "мылить" уже на диафрагмах 5,6 и даже 4, а на 2-2,8 "мылит" и объектив сам по себе, что съедает весь выигрыш от увеличения мегапикселей...
Разрешение. Мифы и реальность. MTF и её измерение.Рассмотрев в общих чертах объективы и матрицы, пора коснуться одной довольно популярной величины, на которую они напрямую влияют - разрешения. Ни один сравнительный обзор не обходится без её обсуждения, в форумах ломаются копья - у чьей камеры оно больше? Попытаемся разобраться, что это такое - разрешение, и заслуживает ли оно таких "почестей". Наши разборки будут напоминать матрёшку - вот, кажется, дошли до сути, а она вновь раскрывает внутри себя другую, и так много раз...

Внешняя матрёшка.

Вновь мегапиксели.
Как и в случае с размером матриц, большинство простой публики (на этот раз конечно не 90, а 60-70% примерно) свято верят, что разрешение измеряется в Мегапикселах. Т.е. 5-мпиксельная камера заведомо детальнее 4-мегапиксельной и так далее. Для многих конкретных камер и конкретных условий это даже верно. Но далеко не для всех. Вспомним определение разрешения (для начала грубое) - это количество мелких деталей которое способен передать снимок. Таким образом, если объектив, скажем, 8-мегапиксельной камеры намазать вазелином, то количество мелких деталей на снимке явно будет меньше чем даже у 3-мегапиксельной камеры. В реальной жизни роль вазелина играют уже упоминавшиеся аберрации, а также переотражения внутри объектива. Как же учесть это всё "одним числом"?. Чтобы не спорить о том какие объекты снимать и какие детали считать, договорились снимать чёрно-белые полоски. Сколько полосок без "смазывания" влезет в кадр (обычно по короткой стороне) - таково и разрешение (обычно в цифровой фотографии, в отличие от старых ГОСТов, одну чёрную линию считают за две - типа "чёрная+белая", типичные значения получаются от 1000 до 1600 линий на высоту кадра). Казалось бы, всё строго - делаем миру (образец с разной частотой полосок), снимаем, считаем полоски и всё. Даже в журналах часто эти цифры публикуют в сравнительных тестах... но, оказывается, что не всё так просто.

Но прежде чем раскрыть вторую матрёшку, оглянемся на первую. Всё-таки - важны мегапиксели или нет? Или дело только в объективе? Ответ прост - мегапиксели всего лишь необходимое, но не достаточное условие. Чтобы разрешить 1000 линий, кадр должен иметь примерно 1500 пикселей в высоту. Этот коэффициент около 1,5 связан с тем, что вероятность "точного попадания" линии миры на линию пикселей близка к нулю. Линии всегда попадают "между", в большей или меньшей степени. Вот из статистического усреднения и берётся этот факт, что для отображения каждых двух линий нужно три ряда пикселей. Таким образом, зная размер кадра можно прикинуть максимально возможное разрешение, которое достигалось бы при идеальном объективе.

Вторая матрёшка.

Линии на высоту.
На пути подсчёта линий нас подстерегают две опасности.
Первая - формальная. Почему-то общепринято считать вертикальное и горизонтальное разрешения. Однако из-за структуры матрицы (расположения пикселей) оказывается, что диагональное примерно в 1,4 раза больше. Этим поспешила воспользоваться одна известная фирма, которая просто повернула матрицу на 45 градусов и назвала модным словом "Супер ЦЦД". С 3 миллионов сенсоров электроника камеры интерполировала 6-мпиксельную картинку. Скептики тут же принялись мерить разрешение своими мирами и с удивлением обнаруживали что таки-да, "дед Мороз существует" - матрица на уровне 5-6мегапиксельных "обычных". Но никто не догадался повернуть миру под 45 градусов - тогда всё станет на свои места - разрешение "обычных" увеличится, а "супер" - снизится, и хвалёные 6 мегапикселей будут на уровне полутора "обычных". А поскольку в реальной жизни редко встречаются ровные параллельные линии, то в среднем разрешение как было на уровне 3-амегапиксельных, так и осталось, что блестяще подтверждается тем фактом, что многие владельцы "волшебных" камер, поиграв с интерполированным разрешением, вернулись на стандартное 3Мп для экономии места на флеш-карте, т.к. не заметили явных улучшений.

Вторая опасность - принципиальная и связана с размытостью понятия "линии различимы". На словах всё выглядит достаточно гладко и понятно. В реальности выясняется, что
1."различимость" линий не дискретна (различимы - неразличимы), а непрерывна - (различимы хорошо, не очень, плохо, очень плохо и т.п.). На самом деле просто плавно падает контраст с единицы до нуля. Поэтому разные наблюдатели видят переход от "плохо различимы" к "практически не различимы" в РАЗНЫХ местах. Этот эффект не зависит от фотосистемы и наблюдается и в плёночной фотографии.
2. в цифровой фотографии кроме этого из-за структуры матрицы добавляются цветные разводы, муар и даже "греческий орнамент", что ещё более усложняет процесс визуального тестирования.

На иллюстрации приведён типичный (не самый сложный) пример. В зависимости от "строгости" наблюдателя колебания разрешения легко достигают 20-40%. В результате ценность цифр, приводимых в обзорах, становится сомнительной. Как мы видели из предыдущей таблицы, максимальные цифры для 3Мп и 5Мп отличаются всего лишь на 30%, поэтому 20-40% - это катастрофически много.

Лирическое отступление.
Похожая ситуация складывается с другими "паспортными" параметрами бытовой техники - например мощностью и частотным диапазоном недорогих аудиосистем. Мощность можно измерять при разных значениях искажений, а нижнюю границу частотного диапазона - при разном падении АЧХ, чем изготовители активно пользуются. В результате мы часто видим пластиковые компьютерные колонки за 50уе с диапазоном от 40Гц и качественные HiFi колонки за 600 уе с диапазоном от 45Гц. Угадайте, у кого из них басы глубже на самом деле?

Аналогия с акустикой не случайна. Действительно, если принять звуковое давление на средних частотах за единицу ("нормировка АЧХ"), то с понижением частоты оно будет плавно падать до нуля и обычно нижней границей называют ту частоту, при которой давление равно либо 0,5, либо 0,25, либо 0,1 (в зависимости от методики, соответственно и результаты - разные). При этом сама АЧХ(Амплитудно-Частотная Характеристика) достаточно объективна и даёт гораздо бОльшее представление чем сухая цифра "границы". Нельзя ли и в оптике вместо "границы" разрешения снять плавную кривую падения контраста при росте частоты штрихов? Именно эта кривая и получила название Modular Transfer Function (MTF) - функция передачи модуляции. Итак, если вместо "классических" штрихов с прямоугольным графиком яркости использовать "синусоидальные", а функцию "контраста" от частоты определить как (Iw-Ib)/(Iw+Ib), где Iw и Ib - яркости изображений "самой белой" и "самой тёмной" точки на данной частоте линий, то MTF(частоты)=КОНТРАСТ(частоты)/КОНТРАСТ(низкой частоты). Таким образом, на низкой частоте MTF равна единице, а с ростом плавно падает до нуля (когда изображения линий сливаются, контраст становится нулевым). Классически определяемое "разрешение" соответствует частоте, при которой MTF становится равной примерно 0,1.

Как и АЧХ в акустике, MTF способна дать гораздо больше информации. Так, два объектива, имеющие одинаковое разрешение (скажем, 1600lph) могут иметь разные графики MTF - у одного график опускается сразу от 50lph вниз, плавно достигая 0,1 при 1600 lph, а у другого держится возле 0,95 "до последнего", и лишь начиная с 1200lph круто падает вниз. При частоте 800-1000lph у первого будет MTF 0,25, а у второго - 0,95. В результате снимки первого будут заметно более вялыми ("мыльными"). Тем не менее формальное разрешение у них действительно одинаково.

Ну уж теперь-то, кажется, всё строго. Измеряем MTF, публикуем сравнение графиков и строим аппараты по ранжиру... Но не будем торопиться. Всё опять не так просто.

Третья матрёшка. MTF.
Измерения и влияние шарпенинга.

Измерить MTF можно даже в домашних условиях. Для этого потребуется всего лишь струйный принтер (720dpi и выше), несколько листов фирменной "струйной" бумаги, а также несколько небольших бесплатных программ, скачанных из Сети. В частности, я снимал графики для нескольких объективов к Canon D60. Результаты для угла кадра представлены ниже (линии на высоту кадра можно получить умножением цифр на оси Х примерно на 30, график просто в привычных "плёночных" координатах):

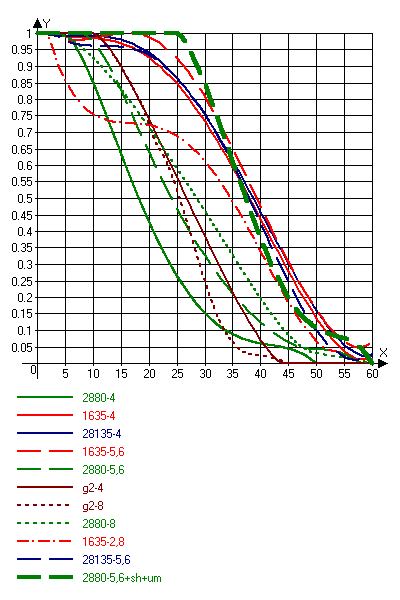Здесь нас интересует сравнение красных и зелёных линий. Красные принадлежат профессиональному объективу 16-35mm/2.8L стоимостью под полторы тысячи долларов. Зелёные - наидешевейшему, наибюджетнейшему пластмассовому 28-80mm/3,5-5,6 за 100 долларов. Если сравнивать тонкие линии - всё логично и "L-ка" оставляет бюджетник далеко позади. Но взгляните на толстый зелёный пунктир! Он отличается от остальных "всего лишь" другими (+1деление) установками шарпенинга на камере (на самом деле - в RAW-конверторе, но это одно и то же) и очень умеренным шарпенингом в Фотошопе (ещё грубо говоря "1 деление"). Но в результате он полностью догнал L-ку! (Понятно, что если применить шарп к L-ке она вновь всех "сделает", но речь сейчас о другом!)

Мы подошли к ключевому моменту. Поставьте себя на место производителя фотокамеры. У Вас есть два пути увеличения разрешения - сделать замечательный резкий объектив уровня L-оптики (+500-1000долларов к цене камеры в зависимости от размера матрицы) или просто "перешить" в её процессоре уровень шарпенинга на одно-два "деления" в большую сторону (бесплатно!!!). Как Вы думаете, что выбирают реальные производители? Разумеется шарпенинг! В результате увеличиваются шумы и понижается реальная чувствительность (если её определять как значение при фиксированном уровне шума). Но это никого не волнует, потому что уровень шума измерять толком не научились, в обзорах он фигурирует редко, а вот высокое разрешение (вместе с мегапикселями и зумом) - сильный маркетинговый козырь. Косвенное подтверждение тому - наличие ISO400 и даже иногда ISO800(!) в камерах с матрицами 1/2,5"! Что мы имеем ещё плохого от "встроенного" шарпенинга, кроме увеличения шумов? Мы имеем, образно говоря, "потолок" детализации. Т.е. дальнейший шарпенинг в Фотошопе больше не приводит к её увеличению без сопутствующих артефактов и искажений, "несовместимых с жизнью", в отличие от камер без встроенного шарпа. Там с помощью Фотошопа иногда можно вполне "догнать" разрешение до "накачанных" лидеров (разумеется ценой того же шума, но у нас по крайней мере есть выбор!).

Последняя матрёшка. Крах разрешения.

Итак, мы пришли к интересному выводу. Измерять MTF (и, как частный случай, - разрешение) можно, но не имеет смысла до тех пор, пока мы не сможем нормировать встроенный шарпенинг. В случае если камеры имеют формат RAW и построены на одинаковых матрицах это сделать просто - выставлением одинаковых параметров конвертора. Но таких случаев очень немного. Во всех же остальных случаях нормирование НЕВОЗМОЖНО. У большинства камер имеется три градации (низкий-норма-высокий), но "низкий" одной может соответствовать "высокому" другой, поэтому установка всех испытуемых в "норму" проблему не решает. Если матрицы одного размера и производителя, можно косвенно судить о шарпе по уровню шумов. Но и тут разная "начинка" камер и разные "фирменные" шумоподавители иногда могут портить картину. Если же шарпинг не нормировать, то всегда даже объективно слабая, но "пошарпленная" камера будет выигрывать в тестах у объективно сильной, но не шарпленной (как в приведённом графике заведомо слабый 28-80 практически выиграл у ВДЕСЯТЕРО более дорогого 16-35L).

Совершенно ясно, что с заменой строгой решётки MTF на реальные кадры проблема разного шарпа никуда не уйдёт и скачивания различных тестовых снимков не помогут, особенно учитывая лёгкость их подделки. Легко можно экспортировать "штамп фотоаппарата"(EXIF) из оригинала в обработанный в фотошопе снимок и выдать его за оригинал. Кроме того, вне обсуждения осталось то, что на разных положениях зума и в разных частях кадра разрешение даже одного и того же объектива существенно разное, и как (и с какими весовыми коэффициентами) его усреднять - тоже вопрос открытый.

Так что же делать? Как сравнивать разрешения?
А плюньте! Не надо их сравнивать! Не в них счастье! Как уже было сказано при обсуждении ГРИП, средний глаз на фото 13*18 различает лишь 1/1500 диагонали, что для фото 15*20 даёт примерно 1000lph(линий на высоту). Таким образом разница между 1200 и 1400 lph в 95% любительских случаев абсолютно несущественна. Гораздо более важны, например, хроматические аберрации, которые на "гиперзумах" просто глазом видно...

ЗАМЕЧАНИЕ1: разумеется вышеприведённый совет относится лишь к изделиям известных оптических фирм нормальной и высокой ценовой категории (от 3 мегапикселей), если же Вы нацелились на некую супердешёвую веб-камеру или мыльницу никому не известной марки "хрен-тек" за десять-двадцать долларов, разрешение проверить абсолютно необходимо. Пластмассовый дверной глазок может давать что угодно :-)
ЗАМЕЧАНИЕ2: понятно что высокое разрешение при прочих равных всегда лучше низкого ("заблюрить" в Фотошопе никогда не поздно), и я не хочу сказать, что оно ВООБЩЕ неважно. Просто на данном историческом этапе и у большинства конкретных доступных на рынке камер оно стоит далеко не на первом месте в качестве критерия выбора.

О триединстве шума, чувствительности и разрешения.

Как мы уже видели выше, от алгоритмов шарпенинга и шумоподавления, встроенных в камеру, зависит "пропорция" между шумом, чувствительностью и разрешением. Т.е. "улучшая" одно, мы "ухудшаем" другое. Как и в большинстве других случаев, нельзя однозначно сказать - что суммарно "лучше" и что "хуже" - это зависит от задач и вкусов (кто-то не выносит "мыла", а кто-то шума). Важно просто понимать это единство и взаимообусловленность. Иногда при сравнении близких по классу камер можно слышать заявления типа "камера А больше мылит, зато меньше шумит, чем камера Б". В таких случаях всегда хочется предложить вместо настроек "по умолчанию" снизить уровень шарпа у камеры Б и повысить - у камеры А. Не исключено что результаты либо сравняются, либо даже "поменяются местами".
Вообще я, к большому сожалению, не видел ещё НИ ОДНОГО грамотного обзора, где всерьёз изучались встроенные установки и предпринималась хоть какая-то попытка выставить их "сопоставимо". Обычно отдельно снимают шум от чувствительности, затем отдельно - сравнивают разрешение при одном и том же ISO и диафрагме. И всё это при настройках "по умолчанию"!

О том, что стандартов на шумы до сих пор толком не выработано, свидетельствует, например, тот факт, что на одном очень уважаемом и серьёзном сетевом фоторесурсе (dpreview.com) они (стандарты) недавно поменялись - т.е. значения для одной и той же камеры в разных парных тестах сильно отличаются.

RAW, TIFF и JPG - в чём разница?Даже если Вы не в ладах с математикой, не пропускайте нижеследующее "математическое отступление" - постарайтесь его понять, т.к. всё дальнейшее изложение будет неоднократно обращаться к полученным там выводам. Профессиональных же математиков я попрошу не судить меня за нестрогость изложения и многократное повторение очевидных вещей. Опыт показывает, что для большинства читателей они не очевидны.

Математическое отступление.

Поговорим о преобразовании функций. Для простоты возьмём функцию F(X)=X на отрезке [0,1]. Легко себе представить её график - это прямая линия под 45 градусов. Теперь применим к ней последовательно пару функций - G1(X)=100*X и G2(X)=0.01*X. Финальная функция G2(G1(F(X)))=0.01*100*X=X очевидно никак не изменилась - всё тот же отрезок под 45 градусов. Таким образом, преобразование G1 было обратимым - оно имеет т.н. обратное преобразование G2. Нетрудно видеть, что и преобразование H1(X)=0.1*X также обратимо и имеет обратное - Н2(Х)=10*X. Кроме этого, и порядок применения обратимых преобразований не важен: G2(G1(F(X)))=G1(G2(F(X))). Всё так хорошо лишь пока мы находимся на "территории математики" - все числа у нас действительные, т.е. могут принимать любые значения и быть измерены с любой точностью.

Но как только от "математических" чисел мы переходим к "компьютерным"(или "цифровым"), т.е. к ячейкам памяти, появляются два фундаментальных ограничения: 1. диапазон ограничен максимальным числом М (т.е. Y 2. точность ограничена числом m (т.е. cуществуют только Y=k*m, где k-натуральное число, а все остальные "округляются" до этих)

Представим что на рассмотренных выше примерах M=1 и m=0.01., кроме этого считаем значения ограниченными снизу нулём.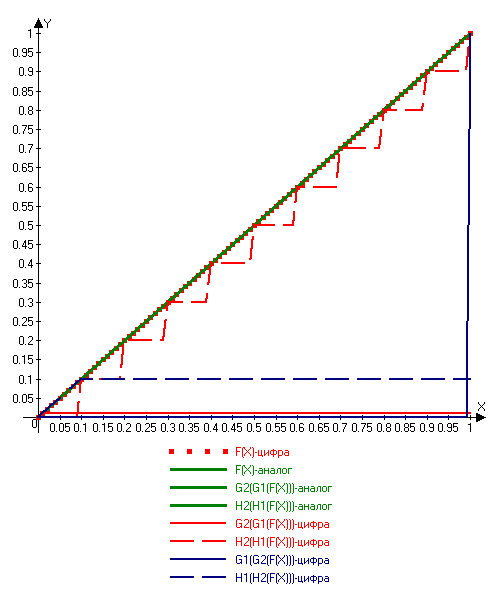

Исходная функция F изменится мало - появятся маленькие "ступеньки" по 0.01 (см График, красные точки)
Применим функцию G1. На всех точках при X>0.01 она "обрежется" до единицы и после применения G2 на всём отрезке кроме нуля результат будет 0.01 (см. График, красная линия)
Применим функцию H1. Вместо ста разных значений Y теперь принимает всего десять, т.к. от 0 до 0.1 можно разместить всего десять отсчётов с точностью m. Применение обратной функции H2 не меняет картину, а лишь увеличивает шаг в десять раз (см. График, красный пунктир)
Применение функций в обратном порядке ("G2 затем G1" и "H2 затем H1") разберите самостоятельно, ответ - на графике синим цветом. Видно, что результат не совпадает ни с чем: ни с функцией F, ни с результатом "прямого" применения пары G1G2 и H1H2.
Легко даже в уме прикинуть результат не только для умножения, но и для сложения, например для последовательного применения J1(X)=X+0.5 и J2(X)=X-0.5.
Обобщим полученные на этом простом примере результаты. Итак, при ограниченном диапазоне значений и ограниченной точности (разрядности) данных, строго говоря, ЛЮБОЕ преобразование МОЖЕТ перестать быть обратимым, и, более того, МОЖЕТ приводить к потере информации. Потеря информации получается ДВУХ сортов: "ограничение" и "потеря разрядности". В приведённом выше примере умножение на 10 (и тем более на 100), а также сложение (и вычитание) 0.5 приводило к "ограничению". А в случае, когда мы сначала делили на 10 (и тем более на 100) - мы видели потерю разрядности.

Поясню выделенное слово "МОЖЕТ". На приведённой в примере функции F(X)=X легко доказать что не только МОЖЕТ, но ВСЕГДА необратимо. Но для некоторых других функций это не так. Например функцию F2(X)=0.1*X можно смело "подвергать" воздействию умножения на 10 - ограничения не произойдёт. Причина - диапазон значений не подходит "достаточно близко к границе". Впрочем, от умножения на 100 это "не спасёт". Другой пример: функцию F3(X)=0.5*X можно безболезненно умножать на два (или прибавлять 0.5), а вот на 10 умножать (или прибавлять 0.8) без ограничения уже не выйдет. Обобщим вновь: чем ближе значения исходной функции к границам диапазона, тем более "мягкими" должны быть преобразования для того, чтобы оставаться обратимыми.

И, наконец, последнее. Выше я показал, что последовательное применение двух преобразований (прямого и обратного) не совпадает в "цифровом" случае с исходным результатом, т.е. с тождественным преобразованием, которому в математике равно последовательное применение прямой и обратной функции. Но если это справедливо даже для тождественного преобразования(частный случай), то совершенно очевиден и более общий случай ЛЮБОГО преобразования, являющегося математической комбинацией двух других: если "в математике" А(В(...))=С(...), то в общем случае "в цифре" A(B(...)) НЕ РАВНО С(...). Иными словами, если к одной и той же цели "математически" можно придти разными путями, то эти же пути "в цифре" дадут строго говоря РАЗНЫЙ результат.

следующая страница